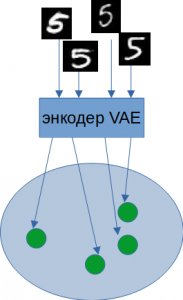
- Принцип работы, отличия от автокодировщиках
- Как реализуется обучение (учитывая, добавление вероятностного слоя)
- Генеративные модели на вариационных автокодировщиках
У вариационных автокодировщиков два скрытых пространства мю(матожидание) и сигма(дисперсия). Поэтому в скрытом пространстве вместо точек, как в автокодировщиках появляются области, что создает непрерывное пространство. Вместо прямой передачи скрытых значений декодеру, VAE используют их для расчета средних значений и стандартных отклонений. Затем вход декодера собирается из соответствующего нормального распределения.

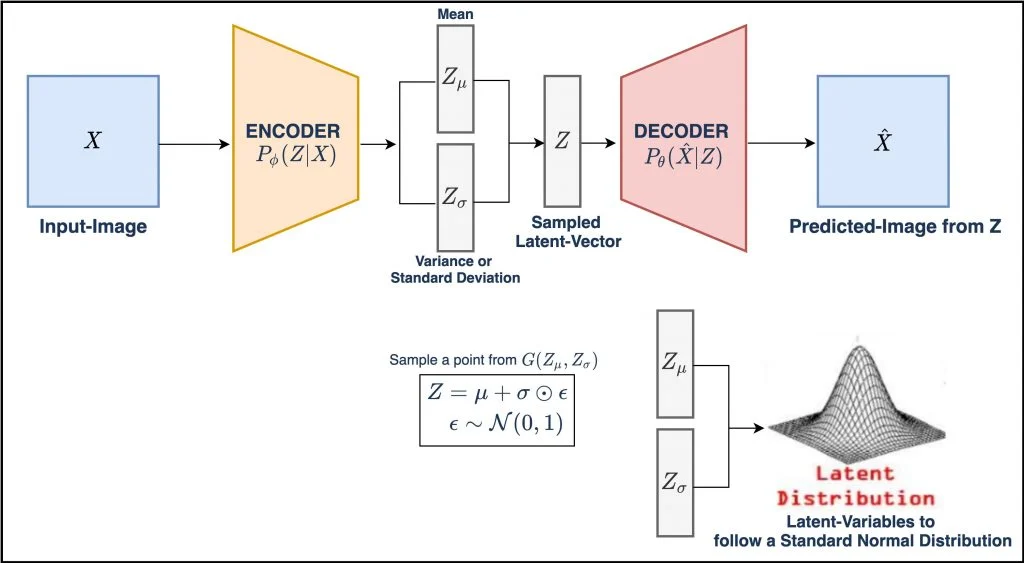
В процессе обучения VAE заставляет это нормальное распределение быть как можно более близким к стандартному нормальному распределению, включая в функцию потерь расстояние Кульбака-Лейблера. VAE будет изменять, или исследовать вариации на гранях, и не случайным образом, а в определенном, желаемом направлении.
Обучение VAE
Чему необходимо обучить VAE:
- Преобразовывать точки из пространства
Xв области в пространствеZ. - Компоновать эти области вместе в одну большую непрерывную область.
Первую задачу можно решить следующим образом. Ранее обычный АЕ для каждого изображения создавал точку в пространстве Z.
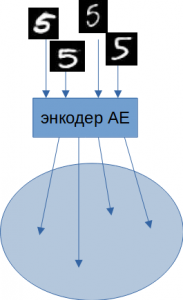
Z с заданными параметрами. Размазывание точки до целой области дает VAE существенный выигрыш при восстановлении похожих изображений.Из описания выше не ясно, как формируются области. Каждое изображение на входе АЕ, проходя через энкодер, порождает одну точку в скрытом пространстве. Но АЕ обучается не на одной эпохе. По мере прохождения обучения проходит множество эпох, и одно и то же изображение сгенерирует множество точек с одинаковыми мат. ожиданием и дисперсией.
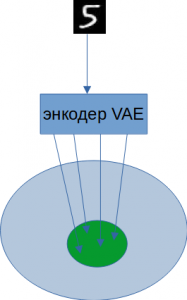
Формирование областей в скрытом пространстве
Решение следующее:
К выходу энкодера параллельно подключим два dense-слоя: один предскажет мат. ожидание, второй – дисперсию (или ее логарифм).
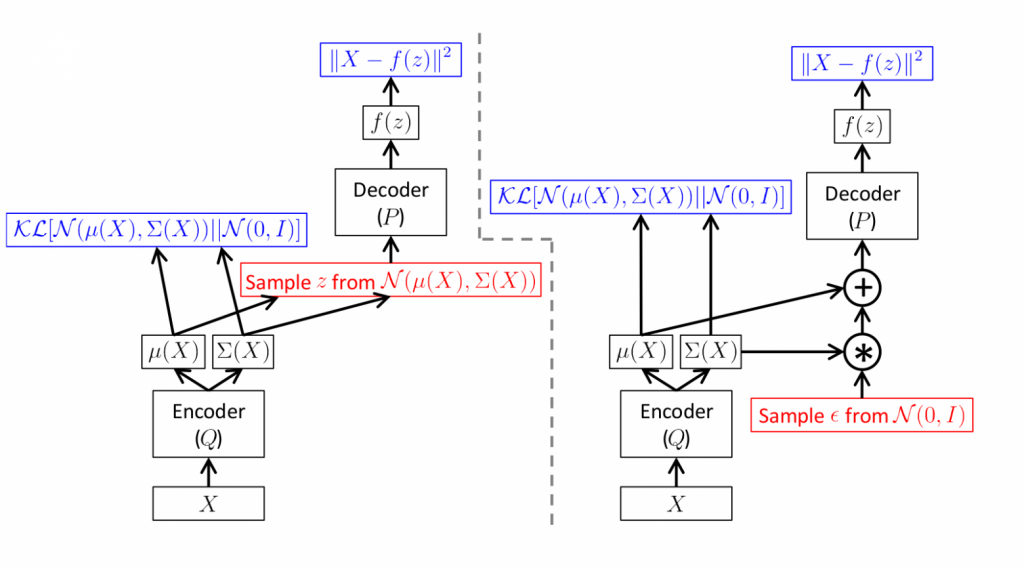
На рисунке ниже представлен фрагмент нейронки, реализующей эту идею. Вариант слева получает от декодера мат. ожидание и дисперсию, генерирует случайный вектор и отдает декодеру. Вариант очевидный, но эту сеть не обучить методом обратного распространения ошибки. Генератор случайных чисел – стохастический компонент сети. Тогда как метод обратного распространения градиента требует, чтобы части сети были детерминированы. Только так удастся итеративно передавать градиенты и применять правило цепочки.
В работе мы будем придерживаться другого (справа) варианта. Энкодер выдает мат. ожидание и дисперсию. Генератор случайных чисел формирует нормальный вектор с нулевым мат. ожиданием и единичной дисперсией. Отдельный слой изменяет параметры распределения на значения, предсказанные энкодером и отдает декодеру. В этом случае на пути обратного распространения градиентов окажутся только детерминированные части сети.
Даже превращение точек пространства Z в области не убирает промежутков между ними. Энкодер не ограничивает значения мат. ожидания и дисперсии. Необходимо дополнительно группировать используемые области в пространстве Z. И в идеале делать это в одну большую непрерывную область. Решением данной проблемы может стать их группировка вокруг некоторого центра.
Потребуем от VAE скомпоновать вместе все используемые области. В этом нам поможет дополнительная функция потерь, а именно — дивергенция Кульбака-Лейблера. Так у автокодировщика появится дополнительный лосс.
Дивергенция Кульбака-Лейблера (дивергенция KL) – это мера того, как одно распределение вероятностей отличается от второго, эталонного распределения вероятностей.
Чтобы скомпоновать точки в скрытом пространстве вокруг некоторого центра часто требуют, чтобы их распределение было нормальным. Здесь мы можем использовать дивергенцию Кульбака-Лейблера. Она покажет, насколько это распределение точек отличается от нормального.
В этом частном случае дивергенция KL имеет вид:
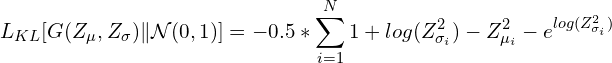
Или:
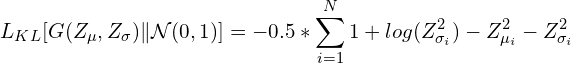
В приведенном выше уравнении Zmu и Zsigma – векторы мат. ожидания и дисперсии скрытого пространства кодировщика. Сумма берется по всем измерениям в скрытом пространстве.
KL-дивергенцию в Numpy можно записать как:
kl_loss = -0.5 * numpy.sum(1 + numpy.log(Z_sigma ** 2) – numpy.square(Z_mean) – numpy.exp(np.log(Z_sigma ** 2), axis = 1)
# или так
kl_loss = -0.5 * numpy.sum(1 + numpy.log(Z_sigma ** 2) – numpy.square(Z_mean) – Z_sigma ** 2, axis = 1)