
Увеличение уровней иерархии в организации увеличивает хаос и ведет к поглощению всех доступных ресурсов. Это неочевидное утверждение было описано советским математиком Владимиром Арнольдом. Ниже сокращенная статья из его брошюры “”Жесткие” и “мягкие” математические модели”.
—
Явление, описываемое в этом разделе, хорошо известно в теории управления техническими системами. Оно наблюдается в чрезвычайно общей ситуации, но здесь я опишу его в самой простой модели, заменяя лишь технические термины человеческими.
Пусть производство какого-либо продукта x управляется некоторым руководителем, принимающим решение о скорости производства:
В свою очередь, поведение руководителя у управляется руководителем второго ранга, принимающим решение о том, как нужно менять скорость производства:
\(Y=dX/dt\)
В свою очередь, поведение руководителя второго ранга z управляется руководителем третьего ранга, и т. д. вплоть до генерального руководителя (ранга n). Генеральный руководитель в нашей модели реализует обратную связь: его решение основывается не на желании выполнить приказ начальства (как у руководителей предыдущих рангов), а на интересах дела. Например, он может желать достичь уровня X величины x и будет влиять на руководителя предыдущего ранга в положительную сторону, если уровень x не достигнут, и в отрицательную — если он превзойден. Например, для n = 3 простейшая модель этого рода имеет вид
\(dX/dt = Y,dY/dt = Z,dZ/dt = -k(x_{0}-X)\)
Эту систему можно переписать в виде линейного дифференциального уравнения порядка n:
\(d^{n}X/dt^{n}=-k(x_{0}-X)\)
Уравнения этой (жесткой) модели легко решаются в явном виде. Устойчивость желаемого стационарного состояния (x= X, y= z= … = 0) определяется тем, отрицательны ли вещественные части корней A характеристического уравнения
\(1^{n}=-k\)
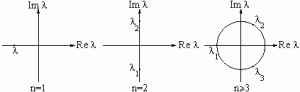
Эти корни — комплексные числа, изображенные на рис. 10. Эти корни образуют на плоскости комплексного переменного l вершины правильного n-угольника. Если n > 3, некоторые вершины обязательно лежат в (неустойчивой) правой полуплоскости (Re l>0). При n =1 корень l=-k лежит в устойчивой полуплоскости, а при n= 2 корни
\((1=\pm i\sqrt{k})\) лежат на границе устойчивости.
Вывод. Многоступенчатое управление, описываемое нашей моделью при n>3, неустойчиво. Двухступенчатое управление приводит к периодическим колебаниям, но не вызывает катастрофического нарастания колебаний, происходящего при трех- и более ступенчатом управлении.
Настоящую устойчивость обеспечивает только одноступенчатое управление, при котором управляющее лицо более заинтересовано в интересах дела, чем в поощрении со стороны начальства.
Эти выводы, сделанные выше на основании анализа простейшей жесткой модели, на самом деле выдерживают проверку на структурную устойчивость, исключая лишь случай n= 2: двухступенчатое управление может оказаться как устойчивым, так и неустойчивым, в зависимости от деталей организации дела, которыми мы выше пренебрегли при составлении нашей самой простой модели…….
_______
Vladimir Arnold – Soft and Hard Mathematical Models, publication of Moscow Center for Continuous Mathematical Education, 2004, page 17- The Danger of Multilevel Management.
_______
Настоящая стабильность возможна только в одноуровневой иерархии, где руководитель заинтересован в результате, а не в желаниях своих руководителей. Реальные организации часто имеют многоуровневую иерархию управления. Долгосрочное выживание таких организаций объясняется тем, что существенные части организации образуют плоские структуры, в которых люди добровольно организуются для совместной работы над общими целями, а не сосредоточены на выполнении инструкций своих менеджеров. Без этих, не заявленных структур, многоуровневая организация разрушится.
—
PS Если вы думаете по-другому попробуйте поуправлять нижним шариком.
146